Linear Regression
Linear Regression is quite a way that will attempt to fit a line through observed variables (x,y). If we look into the graphs it will try to find the line which is more touching to the point (x^i,y^i) for all I in the dataset, y as a linear function of x and it will seem like
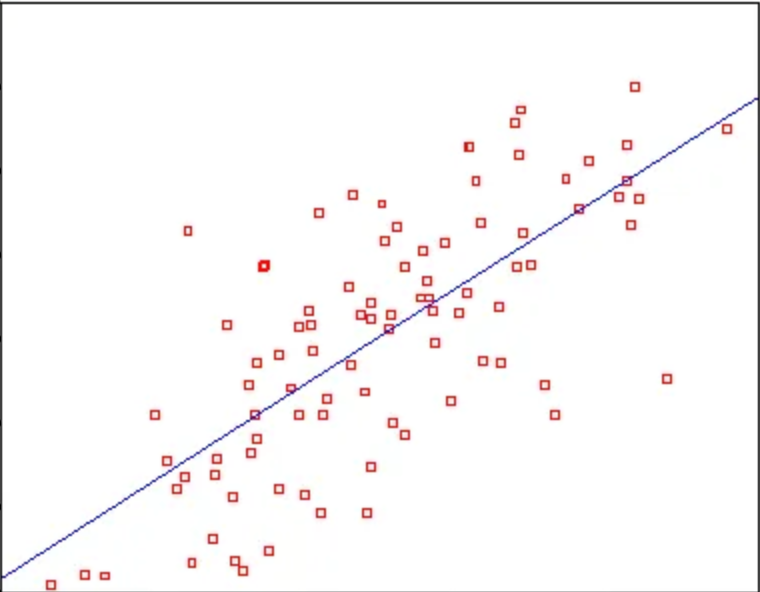
As it will try to prophesy a line most possible it will do by the least-squares method which is going to decrease the squares of the distance from the line for all the points.
Catholic rule of Least Squares
As the method will try to find the line Y = MX+ b and for solving it by math just find the distance from the line by putting the point in the equation and all the distances and just minimize it by taking derivative and assigning it to the zero. The general equation looks like
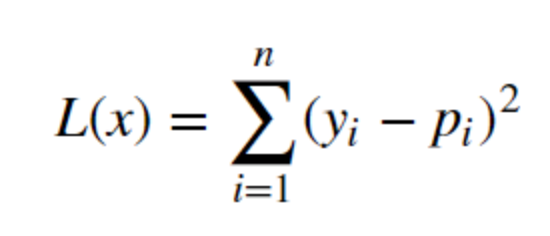
and to view it on the graph it will look like
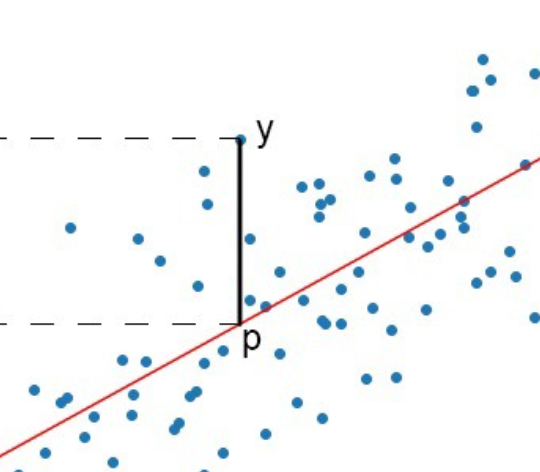
Why we use least squares
One purpose is that the equations required in solving for the best-fit line are easy to solve. The only satisfying reason for using it will be proved by the gauss theorem which states
Suppose y=f(x). We measure values x^i,y^i and compute errors y^i-f(x^i). If these errors are independent and normally distributed, then consider, for any possible linear function f the probability P^f of getting the measurements (x^i,y^i) if y=f(x) were the correct model. The least-squares line is the line for which P^f is maximized.
This is the only best reason why we used it over the other methods.
Future Readings
- Björck, Å. (1996). Numerical Methods for Least Squares Problems. SIAM.
- Kariya, T.; Kurata, H. (2004). Generalized Least Squares. Hoboken
I hope this helps you in understanding you, linear regression easy way.

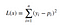
Comments
Post a Comment